函数高考题型分析,函数的高考题

1.11年的浙江高考题，f(x)=x^2-|x+a|为偶函数，则实数a=

2.2道高考题外加1道函数题

3.高1函数解题方法的名称+例题

一、基本概念：

1、 数列的定义及表示方法：

2、 数列的项与项数：

3、 有穷数列与无穷数列：

4、 递增（减）、摆动、循环数列：

5、 数列{an}的通项公式an：

6、 数列的前n项和公式Sn:

7、 等差数列、公差d、等差数列的结构：

8、 等比数列、公比q、等比数列的结构：

二、基本公式：

9、一般数列的通项an与前n项和Sn的关系：an=

10、等差数列的通项公式：an=a1+(n-1)d an=ak+(n-k)d (其中a1为首项、ak为已知的第k项) 当d≠0时，an是关于n的一次式；当d=0时，an是一个常数。

11、等差数列的前n项和公式：Sn= Sn= Sn=

当d≠0时，Sn是关于n的二次式且常数项为0；当d=0时（a1≠0），Sn=na1是关于n的正比例式。

12、等比数列的通项公式： an= a1 qn-1 an= ak qn-k

(其中a1为首项、ak为已知的第k项，an≠0)

13、等比数列的前n项和公式：当q=1时，Sn=n a1 (是关于n的正比例式)；

当q≠1时，Sn= Sn=

三、有关等差、等比数列的结论

14、等差数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等差数列。

15、等差数列{an}中，若m+n=p+q，则

16、等比数列{an}中，若m+n=p+q，则

17、等比数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等比数列。

18、两个等差数列{an}与{bn}的和差的数列{an+bn}、{an-bn}仍为等差数列。

19、两个等比数列{an}与{bn}的积、商、倒数组成的数列

{an bn}、 、 仍为等比数列。

20、等差数列{an}的任意等距离的项构成的数列仍为等差数列。

21、等比数列{an}的任意等距离的项构成的数列仍为等比数列。

22、三个数成等差的设法：a-d,a,a+d；四个数成等差的设法：a-3d,a-d,,a+d,a+3d

23、三个数成等比的设法：a/q,a,aq；

四个数成等比的错误设法：a/q3,a/q,aq,aq3 (为什么？)

24、{an}为等差数列，则 (c>0)是等比数列。

25、{bn}（bn>0）是等比数列，则{logcbn} (c>0且c 1) 是等差数列。

26. 在等差数列 中：

（1）若项数为 ，则

（2）若数为 则， ，

27. 在等比数列 中：

（1） 若项数为 ，则

（2）若数为 则，

四、数列求和的常用方法：公式法、裂项相消法、错位相减法、倒序相加法等。关键是找数列的通项结构。

28、分组法求数列的和：如an=2n+3n

29、错位相减法求和：如an=(2n-1)2n

30、裂项法求和：如an=1/n(n+1)

31、倒序相加法求和：如an=

32、求数列{an}的最大、最小项的方法：

① an+1-an=…… 如an= -2n2+29n-3

② (an>0) 如an=

③ an=f(n) 研究函数f(n)的增减性 如an=

33、在等差数列 中,有关Sn 的最值问题——常用邻项变号法求解：

(1)当 >0,d<0时，满足 的项数m使得 取最大值.

(2)当 <0,d>0时，满足 的项数m使得 取最小值。

在解含绝对值的数列最值问题时,注意转化思想的应用。

六、平面向量

1．基本概念：

向量的定义、向量的模、零向量、单位向量、相反向量、共线向量、相等向量。

2． 加法与减法的代数运算：

(1) ．

(2)若a=（ ）,b=（ ）则a b=（ ）．

向量加法与减法的几何表示：平行四边形法则、三角形法则。

以向量 = 、 = 为邻边作平行四边形ABCD，则两条对角线的向量 = + , = － , = －

且有｜ ｜－｜ ｜≤｜ ｜≤｜ ｜+｜ ｜．

向量加法有如下规律： ＋ = ＋ (交换律); +( +c)=( + )+c （结合律）;

+0= ＋(－ )=0.

3．实数与向量的积：实数 与向量 的积是一个向量。

(1)｜ ｜=｜ ｜·｜ ｜;

(2) 当 ＞0时， 与 的方向相同；当 ＜0时， 与 的方向相反；当 =0时， =0．

(3)若 =（ ），则 · =（ ）．

两个向量共线的充要条件：

(1) 向量b与非零向量 共线的充要条件是有且仅有一个实数 ，使得b= ．

(2) 若 =（ ）,b=（ ）则 ‖b ．

平面向量基本定理：

若e1、e2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量 ，有且只有一对实数 ， ，使得 = e1+ e2．

4．P分有向线段 所成的比：

设P1、P2是直线 上两个点，点P是 上不同于P1、P2的任意一点，则存在一个实数 使 = ， 叫做点P分有向线段 所成的比。

当点P在线段 上时， ＞0；当点P在线段 或 的延长线上时， ＜0；

分点坐标公式：若 = ； 的坐标分别为（ ）,（ ）,（ ）；则 （ ≠－1）， 中点坐标公式： ．

5． 向量的数量积：

（1）．向量的夹角：

已知两个非零向量 与b，作 = , =b,则∠AOB= （ ）叫做向量 与b的夹角。

（2）．两个向量的数量积：

已知两个非零向量 与b，它们的夹角为 ，则 ·b=｜ ｜·｜b｜cos ．

其中｜b｜cos 称为向量b在 方向上的投影．

（3）．向量的数量积的性质：

若 =（ ）,b=（ ）则e· = ·e=｜ ｜cos (e为单位向量);

⊥b ·b=0 （ ，b为非零向量）;｜ ｜= ;

cos = = ．

(4) ．向量的数量积的运算律：

·b=b· ;( )·b= ( ·b)= ·( b);( ＋b)·c= ·c+b·c．

6.主要思想与方法：

本章主要树立数形转化和结合的观点，以数代形，以形观数，用代数的运算处理几何问题，特别是处理向量的相关位置关系，正确运用共线向量和平面向量的基本定理，计算向量的模、两点的距离、向量的夹角，判断两向量是否垂直等。由于向量是一新的工具，它往往会与三角函数、数列、不等式、解几等结合起来进行综合考查，是知识的交汇点。

七、立体几何

1.平面的基本性质：掌握三个公理及推论，会说明共点、共线、共面问题。

能够用斜二测法作图。

2.空间两条直线的位置关系：平行、相交、异面的概念；

会求异面直线所成的角和异面直线间的距离；证明两条直线是异面直线一般用反证法。

3.直线与平面

①位置关系：平行、直线在平面内、直线与平面相交。

②直线与平面平行的判断方法及性质,判定定理是证明平行问题的依据。

③直线与平面垂直的证明方法有哪些？

④直线与平面所成的角：关键是找它在平面内的射影，范围是{00.900}

⑤三垂线定理及其逆定理：每年高考试题都要考查这个定理. 三垂线定理及其逆定理主要用于证明垂直关系与空间图形的度量.如：证明异面直线垂直，确定二面角的平面角，确定点到直线的垂线.

4.平面与平面

(1)位置关系：平行、相交，（垂直是相交的一种特殊情况）

(2)掌握平面与平面平行的证明方法和性质。

(3)掌握平面与平面垂直的证明方法和性质定理。尤其是已知两平面垂直，一般是依据性质定理，可以证明线面垂直。

(4)两平面间的距离问题→点到面的距离问题→

(5)二面角。二面角的平面交的作法及求法：

①定义法，一般要利用图形的对称性；一般在计算时要解斜三角形；

②垂线、斜线、射影法，一般要求平面的垂线好找，一般在计算时要解一个直角三角形。

③射影面积法，一般是二面交的两个面只有一个公共点，两个面的交线不容易找到时用此法?

回

11年的浙江高考题，f(x)=x^2-|x+a|为偶函数，则实数a=

高考数学基础题二次函数、复合函数。

1、二次函数。

二次函数解析式的三种形式：

一般式：f（x）＝ax2＋bx＋c（a≠0）。?

顶点式：f（x）＝a（x－m）2＋n（a≠0）。

零点式：f（x）＝a（x－x1）（x－x2）（a≠0）。?

辨明两个易误点：

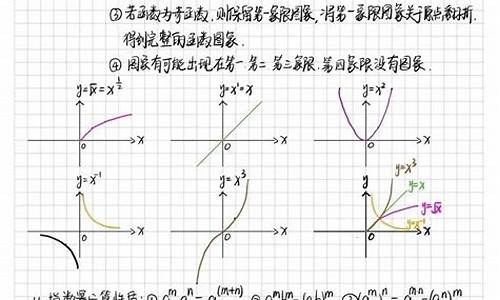
对于函数y＝ax2＋bx＋c，要认为它是二次函数，就必须满足a≠0，当题目条件中未说明a≠0时，就要讨论a＝0和a≠0两种情况。

幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限内，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点。

2、复合函数。

设函数Y=f（u）的定义域为D，函数u=φ（x）的值域为Z，如果D∩Z，则y通过u构成x的函数，称为x的复合函数，记作Y=f（φ（x））。

x为自变量，y为因变量，而u称为中间变量。? 如等都是复合函数。? 就不是复合函数，因为任何x都不能使y有意义。由此可见，不是任何两个函数放在一起都能构成一个复合函数。

高考数学必备技巧：

1、三个“基本”：基本的概念要清楚，基本的规律要熟悉，基本的方法要熟练。

2、做完题目后一定要认真总结，做到举一反三，这样，以后遇到同一类的问题是就不会花费太多的时间和精力了。

3、一定要全面了解数学概念，不能以偏概全。

4、学习概念的最终目的是能运用概念来解决具体问题，因此，要主动运用所学的数学概念来分析，解决有关的数学问题。

5、要掌握各种题型的解题方法，在练习中有意识的地去总结，慢慢地培养适合自己的分析习惯。

6、要主动提高综合分析问题的能力，借助文字阅读去分析理解。

7、在学习中，要有意识地注意知识的迁移，培养解决问题的能力。

8、要将所学知识贯穿在一起形成系统，我们可以运用类比联系法。

9、将各章节中的内容互相联系，不同章节之间互相类比，真正将前后知识融会贯通，连为一体，这样能帮助我们系统深刻地理解知识体系和内容。

10、在数学学习中可以利用口诀将相近的概念或规律进行比较，搞清楚它们的相同点，区别和联系，从而加深理解和记忆。弄清数学知识间的相互联系，透彻理解概念，知道其推导过程，使知识条理化，系统化。

2道高考题外加1道函数题

|-x+a|=|-(x-a)|=|x-a|

f(-x)=f(x)

x^2-|x+a|=(-x)^2-|-x+a|

|x+a|=|-x+a| 对所有x成立

|x+a|=|-x+a| 两边平方得

(x+a)?=(-x+a)? x?+2ax+a?=x?-2ax+a? 4ax=0

ax=0 对所有x成立 只能是a=0

高1函数解题方法的名称+例题

第一题

解:a平方＋2ab+2ac+4bc=12

而:

2bc<=b平方+c平方

所以原式可化简为

a平方＋2ab+2ac+2bc+2bc=12

a平方＋2ab+2ac+2bc+b平方+c平方>=12

(a+b+c)平方>=12

a b c>0

a+b+c>=2根号3

第二题

解:

第一种情况:判别式<=0,=>a^2-4<=0,=>-2<=a<=2

第二种情况:判别式>=0,-a/2<=0,f(0)>=0,

=>a>=2

第三种情况:判别式>=0,-a/2>=1/2,f(1/2)>=0,

=>-5/2<=a<=-2

所以a的最小值为-5/2

第三题解：设f(x)=ax+b,则

f[f(x)]=a(ax+b)+b=a?x+ab+b=4x-1

因此a?=4.........(1)

ab+b=-1..........(2)

由（1）得a=±2.代入（2）式得：

（±2+1）b=-1,∴a=2时，b=-1/3; a=-2时，b=1.

故f(x)=2x-1/3或f(x)=-2x+1.

设f(x)=ax+b

为什么f(f(x))=af(x)+b ?

答：因为将括号内的f(x)看作一个整体，相当于一个x，此时的x=f(x),不知道你明白没？不明白的话可以给我发信息

抽象函数

一般形式为 y=f(x)且无法用数字和字母表示出来的函数，一般出现在题目中，或许有定义域、值域等。

1抽象函数常常与周期函数结合，如：

f(x)=-f(x+2)

f(x)=f(x+4)

2解抽象函数题，通常要用赋值法，而且高考数学中，常常要先求F（0） F（1）

抽象函数的经典题目！！！

我们把没有给出具体解析式的函数称为抽象函数。由于这类问题可以全面考查学生对函数概念和性质的理解，同时抽象函数问题又将函数的定义域，值域，单调性，奇偶性，周期性和图象集于一身，所以在高考中不断出现；如2002年上海高考卷12题，2004年江苏高考卷22题，2004年浙江高考卷12题等。学生在解决这类问题时，往往会感到无从下手，正确率低，本文就这类问题的解法谈一点粗浅的看法。

一．特殊值法:在处理选择题时有意想不到的效果。

例1 定义在R上的函数f(x)满足f (x + y) = f (x) + f ( y )(x，y∈R)，当x<0时，, f (x)>0，则函数f (x)在[a,b]上 ( )

A 有最小值f (a) B有最大值f (b) C有最小值f (b) D有最大值f ( )

分析：许多抽象函数是由特殊函数抽象背景而得到的，如正比例函数f (x)= kx(k≠0)， , , ，可抽象为f (x + y) = f (x) +f (y)，与此类似的还有

特殊函数 抽象函数

f (x)= x f (xy) =f (x) f (y)

f (x)=

f (x+y)= f (x) f (y)

f (x)=

f (xy) = f (x)+f (y)

f (x)= tanx f(x+y)=

此题作为选择题可采用特殊值函数f (x)= kx(k≠0)

∵当x <0时f (x) > 0即kx > 0。.∴k < 0，可得f (x)在[a,b]上单调递减，从而在[a,b]上有最小值f(b)。

二．赋值法．根据所要证明的或求解的问题使自变量取某些特殊值，从而来解决问题。

例2 除了用刚才的方法外,也可采用赋值法

解:令y = -x，则由f (x + y) = f (x) + f (y) (x，y∈R)得f (0) = f (x) +f (-x)…..①,

再令x = y = 0得f(0)= f(0)+ f(0)得f (0)=0，代入①式得f (-x)= -f(x)。

得 f (x)是一个奇函数，再令 ，且 。

∵x <0，f (x) >0，而 ∴ ，则得 ，

即f (x)在R上是一个减函数，可得f (x)在[a,b]上有最小值f(b)。

例3 已知函数y = f (x)(x∈R，x≠0)对任意的非零实数 ， ，恒有f( )=f( )+f( ),

试判断f(x)的奇偶性。

解：令 = -1， =x，得f (-x)= f (-1)+ f (x) ……①为了求f (-1)的值，令 =1， =-1，则f(-1)=f(1)+f(-1),即f(1)=0,再令 = =-1得f(1)=f(-1)+f(-1)=2f(-1) ∴f(-1)=0代入①式得

f(-x)=f(x),可得f(x)是一个偶函数。

三．利用函数的图象性质来解题：

抽象函数虽然没有给出具体的解析式，但可利用它的性质图象直接来解题。

抽象函数解题时常要用到以下结论：

定理1：如果函数y=f(x)满足f(a+x)=f(b-x)，则函数y=f(x)的图象关于x= 对称。

定理2：如果函数y=f(x)满足f(a+x)=f(b+x)，则函数y=f(x)是一个周期函数，周期为a-b。

例4 f(x)是定义在R上的偶函数，且f(x)=f(2-x)，证明f(x)是周期函数。

分析：由 f(x)=f(2-x)，得 f(x)的图象关于x=1对称，又f(x)是定义在R上的偶函数，图象关于y轴对称，根据上述条件，可先画出符合条件的一个图，那么就可以化无形为有形，化抽象为具体。从图上直观地判断，然后再作证明。

由图可直观得T=2,要证其为周期函数，只需证f (x) = f (2 + x)。

证明：f (x) = f (-x) = f [2-(-x)] = f (2 + x)，∴ T=2。

∴f (x)是一个周期函数。

例5 已知定义在[-2，2]上的偶函数，f (x)在区间[0，2]上单调递减，若f (1-m)<f (m),求实数m的取值范围

分析：根据函数的定义域，-m，m∈[-2,2]，但是1- m和m分别在[-2，0]和[0，2]的哪个区间内呢？如果就此讨论，将十分复杂，如果注意到偶函数，则f (x)有性质f（-x)= f (x)=f ( |x| )，就可避免一场大规模讨论。

解：∵f (x)是偶函数， f (1-m)<f(m) 可得 ，∴f(x)在[0，2]上是单调递减的，于是 ，即 化简得-1≤m< 。

采纳我的吧