您现在的位置是: 首页 > 教育新闻 教育新闻
高考抛物线题,高考抛物线秒杀结论
tamoadmin 2024-06-15 人已围观
简介1.设P为抛物线上异于原点O的任意一点,F为抛物线的焦点,直线l:x=—1交x轴于点A,过点1).你应该会.这类题有一个通法:把未知数系数化为0.2)先求AB方程.为:y=x+1.代入y=x^2+mx+2.即:x^2+(m-1)x+1=0Δ=(m-1)^2-4>0知m>3或m<-1.又因为x1,x2属于[0,2].x1+x2=1-m>O.x1x2=1.下面要注意了.(x1-
1.设P为抛物线上异于原点O的任意一点,F为抛物线的焦点,直线l:x=—1交x轴于点A,过点
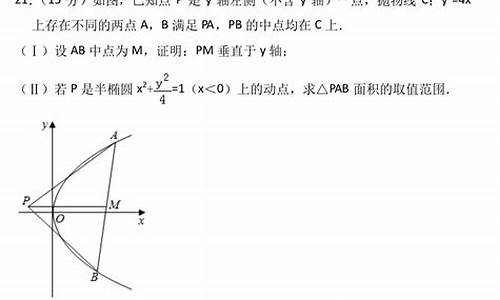
1).你应该会.这类题有一个通法:把未知数系数化为0.
2)先求AB方程.为:y=x+1.
代入y=x^2+mx+2.
即:x^2+(m-1)x+1=0
Δ=(m-1)^2-4>0
知m>3或m<-1.
又因为x1,x2属于[0,2].
x1+x2=1-m>O.
x1x2=1.
下面要注意了.
(x1-2)(x2-2)>0.展开后
x1x2-2(x1+x2)+4>=0
1-2(1-m)+4>=0
所以-3/2=<m<-1(自己能算到这吧).
注意:不能用0<x1+x2<4.0<x1x2<4.
你们老师应该讲过,这样会扩大x1x2的范围
3)有一个公式吧:弦长二:根号下(1+K^2)乘以|x1-x2|.把上面的一带入很容易
第二个看人家的吧!我认为无答案!
如打4分钟则以前需0.36元现需0.33元..不提反降了。
设P为抛物线上异于原点O的任意一点,F为抛物线的焦点,直线l:x=—1交x轴于点A,过点
BF=2,易得B的横坐标为3/2
3/2<√3
即点B应该在点M的左边
所以你这张图是错的,你这张图对应的应该是点B在x轴上方,点A在下方
而你这个解题过程对应的是:点B在x轴下方,点A在x轴上方
此时,直线的斜率应该是大于0的
两种做出来的答案是一样的,自己去试试看吧~~
祝你开心!希望能帮到你,如果不懂,请追问,祝学习进步!O(∩_∩)O
硬算呗,下面开始了
因为y?=2px(x>0)
设P(t^2/2p,t)
所以M(-1,t),N(-1,2p/t)
tan∠MFA=t/(p/2+1)
tan∠NFA=(2p/t)/(p/2+1)
tan∠MFN=tan(∠MFA+∠NFA)=[(2p/t+t)(p/2+1)]/(p/2-1)^2
显然这大于零,所以要使∠MFN最小,tan∠MFN最小,所以2p/t+t最小,此时2p/t=t
所以t^2/2p=1
所以P的纵坐标为1
(以后遇到解析几何题,如发现无明显几何性质,应立即投入计算,别再投机取巧,这是高考趋势(我指的是浙江))









