您现在的位置是: 首页 > 教育改革 教育改革
高考数学函数真题_高考数学函数大题及答案
tamoadmin 2024-05-21 人已围观
简介f(x)=[2sin(x+π/3)+sinx]cosx-3sin?x=[sinx+3cosx+sinx]cosx-3sin?x=2sinxcosx+3cos?x-3sin?x=sin2x+3cos2x=2sin(2x+π/3)1.f(x)的最小正周期=2π/2=π;2.若存在x0属于[0,5π/12],使不等式f(x0)<m成立,即:只需f(x)min<m成立;当x∈[0,5π/12]
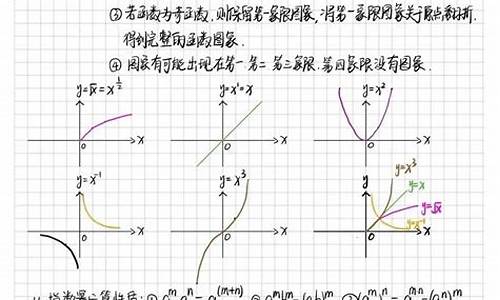
f(x)=[2sin(x+π/3)+sinx]cosx-√3sin?x=[sinx+√3cosx+sinx]cosx-√3sin?x
=2sinxcosx+√3cos?x-√3sin?x=sin2x+√3cos2x=2sin(2x+π/3)
1.f(x)的最小正周期=2π/2=π;
2.若存在x0属于[0,5π/12],使不等式f(x0)<m成立,即:只需f(x)min<m成立;
当x∈[0,5π/12]时,2x+π/3∈[π/3,7π/6],sin(2x+π/3)∈[-1/2,1],
所以 f(x)min=-1,所以:-1<m,即m>-1
实数m的取值范围:m>-1
b^2=c(b+2c)
先变形为 b^2-bc-2c^2=0
再(b+c)(b-2c)=0
因 b、c均为三角形的边,b+c不可能为零
故 b-2c=0
即 b=2c
将cosA=7/8、a=根号6带入三角形的余弦定理a^2=b^2+c^2-2bc cosA
得:b^2+c^2-7/4 bc =6 ----------(*)
再将 b=2c带入(*)式 可得:
c=2
b=4
又由cosA=7/8 可得:
sinA=根号15 /8
所以,三角形ABC的面积是:S=1/2 bc sinA=根号15 /2